lcd panel size calculator factory

The screen size calculator can help you determine the screen dimensions. Have you ever wondered what the statement, the diagonal of the screen is equal to 40" means? How much space does it take up on the wall? What are its height and width? Here you can determine the monitor size or phone screen dimensions. If you"re curious enough, you can even determine how to measure a curved TV screen size!

If you want to find the ideal size of your TV or its distance from your eyes, check out this TV size calculator. Another useful tool is this great projector calculator, which can help in fulfilling your dreams about a home cinema.

Repeat the steps for iPhone 8 Plus, choosing a 16:9 aspect ratio and 5.5-inch diagonal. And what do you get? 4.8" for screen width, 2.7" height, and 12.93 in² screen size. So even though the first iPhone has a longer diagonal, the screen size is smaller than in iPhone 8 plus. (iPhone X also has the big cutout and the curved edges, but we are not taking them into account - even with that simplification, the screen area is smaller).

Our screen size calculator offers the possibility to estimate both a flat and curved screen size. As we"ve already learned how to proceed with a flat monitor, let"s see the differences for a curved one.

How do I measure a curved TV screen size, then? - you may ask. To evaluate the screen"s length, height, and area, we can follow the same equations as for a flat one:

Assuming the screen"s length is the arc length of a circle, we can find the base depth and width by using the following formulas which we use in the screen size calculator:

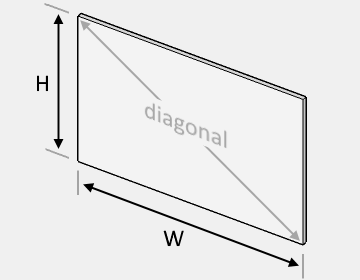
If you"re after the size of the screen"s diagonal, you can either measure it or use Pythagoras" theorem where a & b are the screen"s length and width.

The size of a 16:9 screen depends on how long the screen"s diagonal is, as 16:9 is merely the ratio of the screen"s width to its height. If you have the screens diagonal, you can multiply that measurement by 0.872 to get the screen"s width. You can also multiply the diagonal by 0.49 to get the screen"s height. Then, if you wish to find the screen area, multiply the width by the height.

The aspect ratio of a LCD display is the proportional relationship of its width compared to its height. The two numbers are commonly separated by a colon. The most common aspect ratios are 16:9 (aka widescreen) and 4:3 (closer to the shape of a square monitor, such as old CRT’s and TV’s). It is best to choose a monitor with the same aspect ratio as your video signal. You cannot customize a monitor’s native aspect ratio, so it is critical to know the aspect ratio of your incoming video signal beforehand. Use this handy screen ratio calculator to determine what you need.

TRu-Vu also offers Waterproof Outdoor Monitors, a wide range of Touch Screen Monitors, Medical Displays, Panel-Mount Monitors and Touchscreens, Open-Frame, and 4K Displays. They are all available with 4:3 aspect ratio or 16:9 aspect ratio screens, and standard brightness or Sunlight Readable with at least 1000 nits brightness. All monitors can operate on 12-24VDCor 110-240VAC. We even offer options for Custom OEM LCD Displays. Private Label Monitors is also an option. Sort by size of 7-12″, 13.3-19″, 21.5-65″ Industrial Monitors and Touch Screens. TRU-Vu Monitors also offers a wide range of LCD monitor mounts and stands.

a line of extreme and ultra-narrow bezel LCD displays that provides a video wall solution for demanding requirements of 24x7 mission-critical applications and high ambient light environments

This article is about the electronic device. For mechanical precursors to the modern calculator, see mechanical calculator. For other uses, see Calculator (disambiguation).

An electronic calculator is typically a portable electronic device used to perform calculations, ranging from basic arithmetic to complex mathematics.

The first solid-state electronic calculator was created in the early 1960s. Pocket-sized devices became available in the 1970s, especially after the Intel 4004, the first microprocessor, was developed by Intel for the Japanese calculator company Busicom.

Modern electronic calculators vary from cheap, give-away, credit-card-sized models to sturdy desktop models with built-in printers. They became popular in the mid-1970s as the incorporation of integrated circuits reduced their size and cost. By the end of that decade, prices had dropped to the point where a basic calculator was affordable to most and they became common in schools.

Computer operating systems as far back as early Unix have included interactive calculator programs such as dc and hoc, and interactive BASIC could be used to do calculations on most 1970s and 1980s home computers. Calculator functions are included in most personal digital assistant (PDA) type devices.

In addition to general purpose calculators, there are those designed for specific markets. For example, there are scientific calculators which include trigonometric and statistical calculations. Some calculators even have the ability to do computer algebra. Graphing calculators can be used to graph functions defined on the real line, or higher-dimensional Euclidean space. As of 2016

With the very wide availability of smartphones, tablet computers and personal computers, dedicated hardware calculators, while still widely used, are less common than they once were. In 1986, calculators still represented an estimated 41% of the world"s general-purpose hardware capacity to compute information. By 2007, this had diminished to less than 0.05%.

Electronic calculators contain a keyboard with buttons for digits and arithmetical operations; some even contain "00" and "000" buttons to make larger or smaller numbers easier to enter. Most basic calculators assign only one digit or operation on each button; however, in more specific calculators, a button can perform multi-function working with key combinations.

Calculators usually have liquid-crystal displays (LCD) as output in place of historical light-emitting diode (LED) displays and vacuum fluorescent displays (VFD); details are provided in the section

Large-sized figures are often used to improve readability; while using decimal separator (usually a point rather than a comma) instead of or in addition to vulgar fractions. Various symbols for function commands may also be shown on the display. Fractions such as 1⁄3 are displayed as decimal approximations, for example rounded to 0.33333333. Also, some fractions (such as 1⁄7, which is 0.14285714285714; to 14 significant figures) can be difficult to recognize in decimal form; as a result, many scientific calculators are able to work in vulgar fractions or mixed numbers.

Calculators also have the ability to store numbers into computer memory. Basic calculators usually store only one number at a time; more specific types are able to store many numbers represented in variables. The variables can also be used for constructing formulas. Some models have the ability to extend memory capacity to store more numbers; the extended memory address is termed an array index.

Power sources of calculators are batteries, solar cells or mains electricity (for old models), turning on with a switch or button. Some models even have no turn-off button but they provide some way to put off (for example, leaving no operation for a moment, covering solar cell exposure, or closing their lid). Crank-powered calculators were also common in the early computer era.

The following keys are common to most pocket calculators. While the arrangement of the digits is standard, the positions of other keys vary from model to model; the illustration is an example.

Display panel (output device) – displays input numbers, commands and results. Liquid-crystal displays (LCDs), vacuum fluorescent displays (VFDs), and light-emitting diode (LED) displays use seven segments to represent each digit in a basic calculator. Advanced calculators may use dot matrix displays.

A printing calculator, in addition to a display panel, has a printing unit that prints results in ink onto a roll of paper, using a printing mechanism.

Clock rate of a processor chip refers to the frequency at which the central processing unit (CPU) is running. It is used as an indicator of the processor"s speed, and is measured in clock cycles per second or hertz (Hz). For basic calculators, the speed can vary from a few hundred hertz to the kilohertz range.

The answer, 34 is sent (shifted) back to the X register. From there, it is converted by the binary decoder unit into a decimal number (usually binary-coded decimal), and then shown on the display panel.

Most pocket calculators do all their calculations in binary-coded decimal (BCD) rather than binary. BCD is common in electronic systems where a numeric value is to be displayed, especially in systems consisting solely of digital logic, and not containing a microprocessor. By employing BCD, the manipulation of numerical data for display can be greatly simplified by treating each digit as a separate single sub-circuit. This matches much more closely the physical reality of display hardware—a designer might choose to use a series of separate identical seven-segment displays to build a metering circuit, for example. If the numeric quantity were stored and manipulated as pure binary, interfacing to such a display would require complex circuitry. Therefore, in cases where the calculations are relatively simple, working throughout with BCD can lead to a simpler overall system than converting to and from binary. (For example, CDs keep the track number in BCD, limiting them to 99 tracks.)

Where calculators have added functions (such as square root, or trigonometric functions), software algorithms are required to produce high precision results. Sometimes significant design effort is needed to fit all the desired functions in the limited memory space available in the calculator chip, with acceptable calculation time.

The fundamental difference between a calculator and computer is that a computer can be programmed in a way that allows the program to take different branches according to intermediate results, while calculators are pre-designed with specific functions (such as addition, multiplication, and logarithms) built in. The distinction is not clear-cut: some devices classed as programmable calculators have programming functions, sometimes with support for programming languages (such as RPL or TI-BASIC).

For instance, instead of a hardware multiplier, a calculator might implement floating point mathematics with code in read-only memory (ROM), and compute trigonometric functions with the CORDIC algorithm because CORDIC does not require much multiplication. Bit serial logic designs are more common in calculators whereas bit parallel designs dominate general-purpose computers, because a bit serial design minimizes chip complexity, but takes many more clock cycles. This distinction blurs with high-end calculators, which use processor chips associated with computer and embedded systems design, more so the Z80, MC68000, and ARM architectures, and some custom designs specialized for the calculator market.

In 1642, the Renaissance saw the invention of the mechanical calculator (by Wilhelm SchickardBlaise Pascalarithmetic operations with minimal human intervention.Pascal"s calculator could add and subtract two numbers directly and thus, if the tedium could be borne, multiply and divide by repetition. Schickard"s machine, constructed several decades earlier, used a clever set of mechanised multiplication tables to ease the process of multiplication and division with the adding machine as a means of completing this operation. There is a debate about whether Pascal or Shickard should be credited as the known inventor of a calculating machine due to the differences (like the different aims) of both inventions.Gottfried Leibniz who spent forty years designing a four-operation mechanical calculator, the stepped reckoner, inventing in the process his leibniz wheel, but who couldn"t design a fully operational machine.

The 18th century saw the arrival of some notable improvements, first by Poleni with the first fully functional calculating clock and four-operation machine, but these machines were almost always one of a kind. Luigi Torchi invented the first direct multiplication machine in 1834: this was also the second key-driven machine in the world, following that of James White (1822).Industrial Revolution that real developments began to occur. Although machines capable of performing all four arithmetic functions existed prior to the 19th century, the refinement of manufacturing and fabrication processes during the eve of the industrial revolution made large scale production of more compact and modern units possible. The Arithmometer, invented in 1820 as a four-operation mechanical calculator, was released to production in 1851 as an adding machine and became the first commercially successful unit; forty years later, by 1890, about 2,500 arithmometers had been soldcomptometers.

In 1921, Edith Clarke invented the "Clarke calculator", a simple graph-based calculator for solving line equations involving hyperbolic functions. This allowed electrical engineers to simplify calculations for inductance and capacitance in power transmission lines.

The Curta calculator was developed in 1948 and, although costly, became popular for its portability. This purely mechanical hand-held device could do addition, subtraction, multiplication and division. By the early 1970s electronic pocket calculators ended manufacture of mechanical calculators, although the Curta remains a popular collectable item.

The first mainframe computers, using firstly vacuum tubes and later transistors in the logic circuits, appeared in the 1940s and 1950s. This technology was to provide a stepping stone to the development of electronic calculators.

The Casio Computer Company, in Japan, released the Model 14-A calculator in 1957, which was the world"s first all-electric (relatively) compact calculator. It did not use electronic logic but was based on relay technology, and was built into a desk.

In October 1961, the world"s first all-electronic desktop calculator, the British Bell Punch/Sumlock Comptometer ANITA (A New Inspiration To Arithmetic/Accounting) was announced.vacuum tubes, cold-cathode tubes and Dekatrons in its circuits, with 12 cold-cathode "Nixie" tubes for its display. Two models were displayed, the Mk VII for continental Europe and the Mk VIII for Britain and the rest of the world, both for delivery from early 1962. The Mk VII was a slightly earlier design with a more complicated mode of multiplication, and was soon dropped in favour of the simpler Mark VIII. The ANITA had a full keyboard, similar to mechanical comptometers of the time, a feature that was unique to it and the later Sharp CS-10A among electronic calculators. The ANITA weighed roughly 33 pounds (15 kg) due to its large tube system.Pilot ACE computer project, to lead the development. The ANITA sold well since it was the only electronic desktop calculator available, and was silent and quick.

The tube technology of the ANITA was superseded in June 1963 by the U.S. manufactured Friden EC-130, which had an all-transistor design, a stack of four 13-digit numbers displayed on a 5-inch (13 cm) cathode ray tube (CRT), and introduced Reverse Polish Notation (RPN) to the calculator market for a price of $2200, which was about three times the cost of an electromechanical calculator of the time. Like Bell Punch, Friden was a manufacturer of mechanical calculators that had decided that the future lay in electronics. In 1964 more all-transistor electronic calculators were introduced: Sharp introduced the CS-10A, which weighed 25 kilograms (55 lb) and cost 500,000 yen ($4555.81), and Industria Macchine Elettroniche of Italy introduced the IME 84, to which several extra keyboard and display units could be connected so that several people could make use of it (but apparently not at the same time). The Victor 3900 was the first to use integrated circuits in place of individual transistors, but production problems delayed sales until 1966.

There followed a series of electronic calculator models from these and other manufacturers, including Canon, Mathatronics, Olivetti, SCM (Smith-Corona-Marchant), Sony, Toshiba, and Wang. The early calculators used hundreds of germanium transistors, which were cheaper than silicon transistors, on multiple circuit boards. Display types used were CRT, cold-cathode Nixie tubes, and filament lamps. Memory technology was usually based on the delay-line memory or the magnetic-core memory, though the Toshiba "Toscal" BC-1411 appears to have used an early form of dynamic RAM built from discrete components. Already there was a desire for smaller and less power-hungry machines.

Bulgaria"s ELKA 6521,Sofia. The name derives from ELektronen KAlkulator, and it weighed around 8 kg (18 lb). It is the first calculator in the world which includes the square root function. Later that same year were released the ELKA 22 (with a luminescent display)ELKA 101, was released in 1974. The writing on it was in Roman script, and it was exported to western countries.

The first desktop programmable calculators were produced in the mid-1960s. They included the Mathatronics Mathatron (1964) and the Olivetti Programma 101 (late 1965) which were solid-state, desktop, printing, floating point, algebraic entry, programmable, stored-program electronic calculators.

Another early programmable desktop calculator (and maybe the first Japanese one) was the Casio (AL-1000) produced in 1967. It featured a nixie tubes display and had transistor electronics and ferrite core memory.

The branch instruction was an implied unconditional branch (GOTO) at the end of the operation stack, returning the program to its starting instruction. Thus, it was not possible to include any conditional branch (IF-THEN-ELSE) logic. During this era, the absence of the conditional branch was sometimes used to distinguish a programmable calculator from a computer.

The electronic calculators of the mid-1960s were large and heavy desktop machines due to their use of hundreds of transistors on several circuit boards with a large power consumption that required an AC power supply. There were great efforts to put the logic required for a calculator into fewer and fewer integrated circuits (chips) and calculator electronics was one of the leading edges of semiconductor development. U.S. semiconductor manufacturers led the world in large scale integration (LSI) semiconductor development, squeezing more and more functions into individual integrated circuits. This led to alliances between Japanese calculator manufacturers and U.S. semiconductor companies: Canon Inc. with Texas Instruments, Hayakawa Electric (later renamed Sharp Corporation) with North-American Rockwell Microelectronics (later renamed Rockwell International), Busicom with Mostek and Intel, and General Instrument with Sanyo.

By 1970, a calculator could be made using just a few chips of low power consumption, allowing portable models powered from rechargeable batteries. The first handheld calculator was a 1967 prototype called Cal Tech, whose development was led by Jack Kilby at Texas Instruments in a research project to produce a portable calculator. It could add, multiply, subtract, and divide, and its output device was a paper tape.

The first commercially produced portable calculators appeared in Japan in 1970, and were soon marketed around the world. These included the Sanyo ICC-0081 "Mini Calculator", the Canon Pocketronic, and the Sharp QT-8B "micro Compet". The Canon Pocketronic was a development from the "Cal-Tech" project. It had no traditional display; numerical output was on thermal paper tape.

Sharp put in great efforts in size and power reduction and introduced in January 1971 the Sharp EL-8, also marketed as the Facit 1111, which was close to being a pocket calculator. It weighed 1.59 pounds (721 grams), had a vacuum fluorescent display, rechargeable NiCad batteries, and initially sold for US$395.

However, integrated circuit development efforts culminated in early 1971 with the introduction of the first "calculator on a chip", the MK6010 by Mostek,vacuum fluorescent display, LED, and LCD), led within a few years to the cheap pocket calculator available to all.

In 1971, Pico ElectronicsGeneral Instrument also introduced their first collaboration in ICs, a full single chip calculator IC for the Monroe Royal Digital III calculator. Pico was a spinout by five GI design engineers whose vision was to create single chip calculator ICs. Pico and GI went on to have significant success in the burgeoning handheld calculator market.

The first truly pocket-sized electronic calculator was the Busicom LE-120A "HANDY", which was marketed early in 1971.Mostek MK6010, and the first electronic calculator to run off replaceable batteries. Using four AA-size cells the LE-120A measures 4.9 by 2.8 by 0.9 inches (124 mm × 71 mm × 23 mm).

The first European-made pocket-sized calculator, DB 800Digitron in Buje, Croatia (former Yugoslavia) with four functions and an eight-digit display and special characters for a negative number and a warning that the calculation has too many digits to display.

The first American-made pocket-sized calculator, the Bowmar 901B (popularly termed The Bowmar Brain), measuring 5.2 by 3.0 by 1.5 inches (132 mm × 76 mm × 38 mm), came out in the Autumn of 1971, with four functions and an eight-digit red LED display, for US$240, while in August 1972 the four-function Sinclair Executive became the first slimline pocket calculator measuring 5.4 by 2.2 by 0.35 inches (137.2 mm × 55.9 mm × 8.9 mm) and weighing 2.5 ounces (71 g). It retailed for around £79 (US$194 at the time). By the end of the decade, similar calculators were priced less than £5 ($6.85). Following protracted development over the course of two years including a botched partnership with Texas Instruments, Eldorado Electrodata released five pocket calculators in 1972. One called the Touch Magic was "no bigger than a pack of cigarettes" according to Administrative Management.

One of the first low-cost calculators was the Sinclair Cambridge, launched in August 1973. It retailed for £29.95 ($41.03), or £5 ($6.85) less in kit form. The Sinclair calculators were successful because they were far cheaper than the competition; however, their design led to slow and inaccurate computations of transcendental functions.

Meanwhile, Hewlett-Packard (HP) had been developing a pocket calculator. Launched in early 1972, it was unlike the other basic four-function pocket calculators then available in that it was the first pocket calculator with scientific functions that could replace a slide rule. The $395 HP-35, along with nearly all later HP engineering calculators, uses reverse Polish notation (RPN), also called postfix notation. A calculation like "8 plus 5" is, using RPN, performed by pressing 8, Enter↑, 5, and +; instead of the algebraic infix notation: 8, +, 5, =. It had 35 buttons and was based on Mostek Mk6020 chip.

In 1973, Texas Instruments (TI) introduced the SR-10, (SR signifying slide rule) an algebraic entry pocket calculator using scientific notation for $150. Shortly after the SR-11 featured an added key for entering pi (π). It was followed the next year by the SR-50 which added log and trig functions to compete with the HP-35, and in 1977 the mass-marketed TI-30 line which is still produced.

The first programmable pocket calculator was the HP-65, in 1974; it had a capacity of 100 instructions, and could store and retrieve programs with a built-in magnetic card reader. Two years later the HP-25C introduced CMOS memory during power-off. In 1979, HP released the first expandable calculator, the HP-41C. It could be expanded with random-access memory (RAM, for memory) and read-only memory (ROM, for software) modules, and peripherals like bar code readers, microcassette and floppy disk drives, paper-roll thermal printers, and miscellaneous communication interfaces (RS-232, HP-IL, HP-IB).

The first Soviet pocket battery-powered programmable calculator, Elektronika Elektronika B3-34 wasn"t backward compatible with B3-21, even if it kept the reverse Polish notation (RPN). Thus B3-34 defined a new command set, which later was used in a series of later programmable Soviet calculators. Despite very limited abilities (98 bytes of instruction memory and about 19 stack and addressable registers), people managed to write all kinds of programs for them, including adventure games and libraries of calculus-related functions for engineers. Hundreds, perhaps thousands, of programs were written for these machines, from practical scientific and business software, which were used in real-life offices and labs, to fun games for children. The Elektronika MK-52 calculator (using the extended B3-34 command set, and featuring internal EEPROM memory for storing programs and external interface for EEPROM cards and other periphery) was used in Soviet spacecraft program (for Soyuz TM-7 flight) as a backup of the board computer.

This series of calculators was also noted for a large number of highly counter-intuitive mysterious undocumented features, somewhat similar to "synthetic programming" of the American HP-41, which were exploited by applying normal arithmetic operations to error messages, jumping to nonexistent addresses and other methods. A number of respected monthly publications, including the popular science magazine Наука и жизнь, Science and Life), featured special columns, dedicated to optimization methods for calculator programmers and updates on undocumented features for hackers, which grew into a whole esoteric science with many branches, named "yeggogology" ("еггогология"). The error messages on those calculators appear as a Russian word "YEGGOG" ("ЕГГОГ") which, unsurprisingly, is translated to "Error".

Through the 1970s the hand-held electronic calculator underwent rapid development. The red LED and blue/green vacuum fluorescent displays consumed a lot of power and the calculators either had a short battery life (often measured in hours, so rechargeable nickel-cadmium batteries were common) or were large so that they could take larger, higher capacity batteries. In the early 1970s liquid-crystal displays (LCDs) were in their infancy and there was a great deal of concern that they only had a short operating lifetime. Busicom introduced the Busicom LE-120A "HANDY" calculator, the first pocket-sized calculator and the first with an LED display, and announced the Busicom LC with LCD. However, there were problems with this display and the calculator never went on sale. The first successful calculators with LCDs were manufactured by Rockwell International and sold from 1972 by other companies under such names as: Dataking LC-800, Harden DT/12, Ibico 086, Lloyds 40, Lloyds 100, Prismatic 500 (a.k.a. P500), Rapid Data Rapidman 1208LC. The LCDs were an early form using the Dynamic Scattering Mode DSM with the numbers appearing as bright against a dark background. To present a high-contrast display these models illuminated the LCD using a filament lamp and solid plastic light guide, which negated the low power consumption of the display. These models appear to have been sold only for a year or two.

A more successful series of calculators using a reflective DSM-LCD was launched in 1972 by Sharp Inc with the Sharp EL-805, which was a slim pocket calculator. This, and another few similar models, used Sharp"s Calculator On Substrate (COS) technology. An extension of one glass plate needed for the liquid crystal display was used as a substrate to mount the needed chips based on a new hybrid technology. The COS technology may have been too costly since it was only used in a few models before Sharp reverted to conventional circuit boards.

In the mid-1970s the first calculators appeared with field-effect, twisted nematic (TN) LCDs with dark numerals against a grey background, though the early ones often had a yellow filter over them to cut out damaging ultraviolet rays. The advantage of LCDs is that they are passive light modulators reflecting light, which require much less power than light-emitting displays such as LEDs or VFDs. This led the way to the first credit-card-sized calculators, such as the Casio Mini Card LC-78 of 1978, which could run for months of normal use on button cells.

There were also improvements to the electronics inside the calculators. All of the logic functions of a calculator had been squeezed into the first "calculator on a chip" integrated circuits (ICs) in 1971, but this was leading edge technology of the time and yields were low and costs were high. Many calculators continued to use two or more ICs, especially the scientific and the programmable ones, into the late 1970s.

The power consumption of the integrated circuits was also reduced, especially with the introduction of CMOS technology. Appearing in the Sharp "EL-801" in 1972, the transistors in the logic cells of CMOS ICs only used any appreciable power when they changed state. The LED and VFD displays often required added driver transistors or ICs, whereas the LCDs were more amenable to being driven directly by the calculator IC itself.

With this low power consumption came the possibility of using solar cells as the power source, realised around 1978 by calculators such as the Royal Solar 1, Sharp EL-8026, and Teal Photon.

The interior of a Casio fx-20 scientific calculator from the mid-1970s, using a VFD. The processor integrated circuit (IC) is made by NEC (marked μPD978C). Discrete electronic components like capacitors and resistors and the IC are mounted on a printed circuit board (PCB). This calculator uses a battery pack as a power source.

The processor chip (integrated circuit package) inside a 1980s Sharp pocket calculator, marked SC6762 1•H. An LCD is directly under the chip. This was a PCB-less design. No discrete components are used. The battery compartment at the top can hold two button cells.

Inside a Casio scientific calculator from the mid-1990s, showing the processor chip (small square; top-middle; left), keypad contacts, right (with matching contacts on the left), the back of the LCD (top; marked 4L102E), battery compartment, and other components. The solar cell assembly is under the chip.

The interior of a newer (c.2000) pocket calculator. It uses a button battery in combination with a solar cell. The processor is a "Chip on Board" type, covered with dark epoxy.

At the start of the 1970s, hand-held electronic calculators were very costly, at two or three weeks" wages, and so were a luxury item. The high price was due to their construction requiring many mechanical and electronic components which were costly to produce, and production runs that were too small to exploit economies of scale. Many firms saw that there were good profits to be made in the calculator business with the margin on such high prices. However, the cost of calculators fell as components and their production methods improved, and the effect of economies of scale was felt.

By 1976, the cost of the cheapest four-function pocket calculator had dropped to a few dollars, about 1/20 of the cost five years before. The results of this were that the pocket calculator was affordable, and that it was now difficult for the manufacturers to make a profit from calculators, leading to many firms dropping out of the business or closing. The firms that survived making calculators tended to be those with high outputs of higher quality calculators, or producing high-specification scientific and programmable calculators.

The Elektronika MK-52 was a programmable RPN-style calculator that accepted extension modules; it was manufactured in the Soviet Union from 1985 to 1992

The first calculator capable of symbolic computing was the HP-28C, released in 1987. It could, for example, solve quadratic equations symbolically. The first graphing calculator was the Casio fx-7000G released in 1985.

The two leading manufacturers, HP and TI, released increasingly feature-laden calculators during the 1980s and 1990s. At the turn of the millennium, the line between a graphing calculator and a handheld computer was not always clear, as some very advanced calculators such as the TI-89, the Voyage 200 and HP-49G could differentiate and integrate functions, solve differential equations, run word processing and PIM software, and connect by wire or IR to other calculators/computers.

The HP 12c financial calculator is still produced. It was introduced in 1981 and is still being made with few changes. The HP 12c featured the reverse Polish notation mode of data entry. In 2003 several new models were released, including an improved version of the HP 12c, the "HP 12c platinum edition" which added more memory, more built-in functions, and the addition of the algebraic mode of data entry.

Calculated Industries competed with the HP 12c in the mortgage and real estate markets by differentiating the key labeling; changing the "I", "PV", "FV" to easier labeling terms such as "Int", "Term", "Pmt", and not using the reverse Polish notation. However, CI"s more successful calculators involved a line of construction calculators, which evolved and expanded in the 1990s to present. According to Mark Bollman,

Personal computers often come with a calculator utility program that emulates the appearance and functions of a calculator, using the graphical user interface to portray a calculator. One such example is Windows Calculator. Most personal data assistants (PDAs) and smartphones also have such a feature.

In most countries, students use calculators for schoolwork. There was someelementary arithmetic skills would suffer.in the head, with some curricula restricting calculator use until a certain level of proficiency has been obtained, while others concentrate more on teaching estimation methods and problem-solving. Research suggests that inadequate guidance in the use of calculating tools can restrict the kind of mathematical thinking that students engage in.UK"s Minister of State for Schools, Nick Gibb, voiced concern that children can become "too dependent" on the use of calculators.Curriculum.National Council of Teachers of Mathematics (NCTM) standards and actively promoted the use of classroom calculators from kindergarten through high school.

Ball, Guy; Flamm, Bruce. "The History of Pocket Electronic Calculators". vintagecalculators.com. Vintage Calculators Web Museum. Archived from the original on 3 July 2014. Retrieved 8 July 2014.

Electronic Calculator Invented 40 Years Ago Archived 2008-12-05 at the Wayback Machine All Things Considered, NPR, 30 September 2007. Audio interview with one of the inventors.

"50 Jahre Taschenrechner – Die Erfindung, die niemand haben wollte" [50th anniversary of calculators – the invention not wanted by anyone]. Wirtschaft (in German). Frankfurter Allgemeine Zeitung (FAZ). 27 March 2017. Archived from the original on 29 March 2017. Retrieved 30 March 2017.

Okon, Thomas (27 March 2017). "The First Handheld Digital Calculator Celebrates 50 Years". Electronic Design. Archived from the original on 13 April 2017.

Bellotto, Sam Jr. (August 1972). "Calculators: They Just Keep Multiplying". Administrative Management. Geyer-McAllister Publications. 33 (8): 68–73 – via the Internet Archive.

Reversing Sinclair"s amazing 1974 calculator hack – half the ROM of the HP-35, Ken Shirriff, 2013. See in particular the section "Limited performance and accuracy". For more coverage of Shirriff"s results, see Sharwood, Simon (2 September 2013), "Google chap reverse engineers Sinclair Scientific Calculator", The Register, archived from the original on 23 August 2017

Vasagar, Jeevan; Shepherd, Jessica (1 December 2011). "Subtracting calculators adds to children"s maths abilities, says minister". Archived from the original on 9 March 2016. Retrieved 7 December 2011. The use of calculators will be looked at as part of a national curriculum review, after the schools minister, Nick Gibb, expressed concern that children"s mental and written arithmetic was suffering because of reliance on the devices. Gibb said: "Children can become too dependent on calculators if they use them at too young an age. They shouldn"t be reaching for a gadget every time they need to do a simple sum. [...]"

Hamrick, Kathy B. (October 1996). "The History of the Hand-Held Electronic Calculator". The American Mathematical Monthly. The American Mathematical Monthly, Vol. 103, No. 8. 103 (8): 633–639. doi:10.2307/2974875. JSTOR 2974875.

Miniature electronic calculator – J. S. Kilby, Texas Instruments, 1974 (originally filed 1967), handheld (3 pounds (1.4 kg)) battery operated electronic device with thermal printer

The Japanese Patent Office granted a patent in June 1978 to Texas Instruments (TI) based on US patent 3819921, notwithstanding objections from 12 Japanese calculator manufacturers. This gave TI the right to claim royalties retroactively to the original publication of the Japanese patent application in August 1974. A TI spokesman said that it would actively seek what was due, either in cash or technology cross-licensing agreements. 19 other countries, including the United Kingdom, had already granted a similar patent to Texas Instruments. – New Scientist, 17 August 1978 p455, and Practical Electronics (British publication), October 1978 p1094.

Collectors Guide to Pocket Calculators. by Guy Ball and Bruce Flamm, 1997, ISBN 1-888840-14-5 – includes an extensive history of early pocket calculators and highlights over 1,500 different models from the early 1970s. Book still in print.

Suydam, Marilyn N. (December 1980). Calculators: A Categorized Compilation of References. Supplement 1 (PDF). Columbus, Ohio, USA: Calculator Information Center, Ohio State University. ED199087. SE034434. Archived (PDF) from the original on 19 September 2021. Retrieved 16 October 2022. (64 pages)

LED high-definition full-color display unit is the box, the box is composed of a certain number of LED modules. Therefore, the choice of a model of LED display screen, will be based on the size of the area or length, so as to calculate the number of boxes and modules required. So here, the size calculation of full-color LED display module is introduced, which is convenient for you to understand.

Above is the calculation method of LED HD full-color display module size. If you want to know more about the price and size of the display screen and box module, you can contact us. In addition, it is worth noting that when making the product quotation and goods list, LED display manufacturers will involve the size and quantity of boxes and modules, in order to facilitate customers to clearly understand the contents of the list.

LCD display doesn’t operate the same way as CRT displays , which fires electrons at a glass screen, a LCD display has individual pixels arranged in a rectangular grid. Each pixel has RGB(Red, Green, Blue) sub-pixel that can be turned on or off. When all of a pixel’s sub-pixels are turned off, it appears black. When all the sub-pixels are turned on 100%, it appears white. By adjusting the individual levels of red, green, and blue light, millions of color combinations are possible

The pixels of the LCD screen were made by circuitry and electrodes of the backplane. Each sub-pixel contains a TFT (Thin Film Transistor) element.  These structures are formed by depositing various materials (metals and silicon) on to the glass substrate that will become one part of the complete display “stack,” and then making them through photolithography. For more information about TFT LCDs, please refer to “

The etched pixels by photolith process are the Native Resolution. Actually, all the flat panel displays, LCD, OLED, Plasma etc.) have native resolution which are different from CRT monitors

Although we can define a LCD display with resolution, a Full HD resolution on screen size of a 15” monitor or a 27” monitor will show different. The screen “fineness” is very important for some application, like medical, or even our cell phone. If the display “fineness” is not enough, the display will look “pixelized” which is unable to show details.

PPI stands for number of pixels per inch. It is kind of pixel density. PPI describes the resolution of a digital image, not a print. PPI is used to resize images in preparation for printing

But you see other lower resolution available, that is because video cards are doing the trick. A video card can display a lower LCD screen resolution than the LCD’s built-in native resolution. The video cards can combine the pixels and turn a higher resolution into lower resolution, or just use part of the full screen. But video cards can’t do the magic to exceed the native resolution.

The cost of TVs depends heavily on their size, with larger ones being progressively more expensive. I examine this relationship by aggregating TV price data over a range of sizes and brands. In addition, I clarify how to calculate TV screen area, height, and width. Though TV screens are universally described by the length of their diagonal, I argue that area is a more intuitive parameter for comparing their sizes.

To collect data for this investigation, I consulted The TV section of Walmart’s Canadian website. Here I found 138 TVs listed with screen diagonals ranging from 19” to 75”. I recorded the size and cost of each, summarized in the graph below.

As expected, price increases with TV size. However, size alone isn’t a tremendous predictor. For instance, there were two 32” screen TVs available which were more expensive than many of the 65” screens. We can account for this through the many features which TV models differ in, beyond size. For instance, some have curved screens, some are smart TVs, and others provide 4K ultra HD. Looking at this graph, the distribution of TV models across size is also interesting. Screen diagonals of 50”, 55”, and 65” are by far most abundant. Nevertheless, the confounding factors make it is hard to isolate the contribution of physical size to TV prices from these data. In particular, we’d require the assumption that expensive TV features are equally represented across the sizes.

To tease out the relationship between TV size and price, we must compare TVs which are identical in every way except size. Fortunately, it is possible to do this: some companies sell series of TV models which offer the same features at multiple screen sizes. Although this greatly limits the data available, it does conveniently remove the confounding factors. I selected four TV series: two by Samsung (NU6900 and Tizen Smart LED) and two by LG (UK6090 and UK6300).

Each series follows a consistent trend, but direct comparison of them is challenging since they have different intrinsic values. In the interest of fully covering the range of screen sizes, it was necessary to combine the data. I normalized the prices within each series to facilitate direct comparison. Each set contained a 50” screen, so I normalized the prices by scaling the 50” option to a value of ‘1’. For instance, The LG UK6300 series costed $448 (43”), $548 (50”), $648 (55”), and $998 (65”). I normalized these prices to 0.82, 1.00, 1.18, and 1.82, respectively. This approach was successful in making each series comparable.

Here a clear relationship emerges between cost and TV screen diagonal length. Interestingly, this relationship is not linear, note the curvature of the apparent trend. As TV screen diagonal is increased, further improvements in size become increasingly costly. We can explain this nonlinearity, to do so we must review how screen diagonal is related to its area.

The size and shape of TV screens are specified by the length of the diagonal across the screen and the aspect ratio. Despite this, I believe that screen area is a much more intuitive unit for comparing TV sizes. The screen of a TV is rectangular, so we can find its area by multiplying the length of its height (H) and width (W).

There is a strong linear correlation between cost and screen area (R^2=0.97). For comparison, correlating cost with screen diagonal gave an inferior fit (R^2=0.88). A notable exception to this trend is the outlier at 75” diagonal length (red data point). The deviation at this large size is likely due to current manufacturing limitations, driving up the cost. According to the vice president of TV product marketing at Samsung, there are very few fabrication plants currently operating that are optimized for producing LCD panels of this size.

Having established the relationship between TV screen area and cost using controlled data, we can return to the total data set to gain more insights about TV prices. There was a large range of prices at each TV size, mostly due to the presence or absence of various features in the different models. If the availability of such features is fairly equal across TV sizes, averaging the prices at each size may largely cancel out this variability. I tried this, and it afforded a surprisingly strong linear correlation with screen area.

​Given that these data are from averaging all of the TVs sold by Walmart, this is an impressive fit (R^2=0.89). Conversely, these data were less strongly correlated with screen diagonal (R^2=0.79). There are several implications of this. Firstly, it suggests my earlier observation that TV price is proportional to screen area is broadly applicable. In addition, it implies that expensive TV features are near equally represented across the range of sizes. Lastly, the 75” TVs are an outlier from this trend (red data point), reinforcing that this size of TV is disproportionally expensive in the current market.

The fairness of these prices may come as a surprise to many consumers, since each additional increase in diagonal length appears progressively more expensive. I have shown that this is merely a consequence of the relationship between diagonal length and area. Though geometrically straightforward, some consumers may not have considered this point. It is unfortunate that screen area is not widely used for comparing TV sizes. In addition to being more intuitive, it also simplifies comparing TVs of different aspect ratios. Though most modern TVs have a 16:9 aspect ratio, older TVs usually had a 4:3 ratio. In such cases comparison of diagonal lengths is particularly misleading.