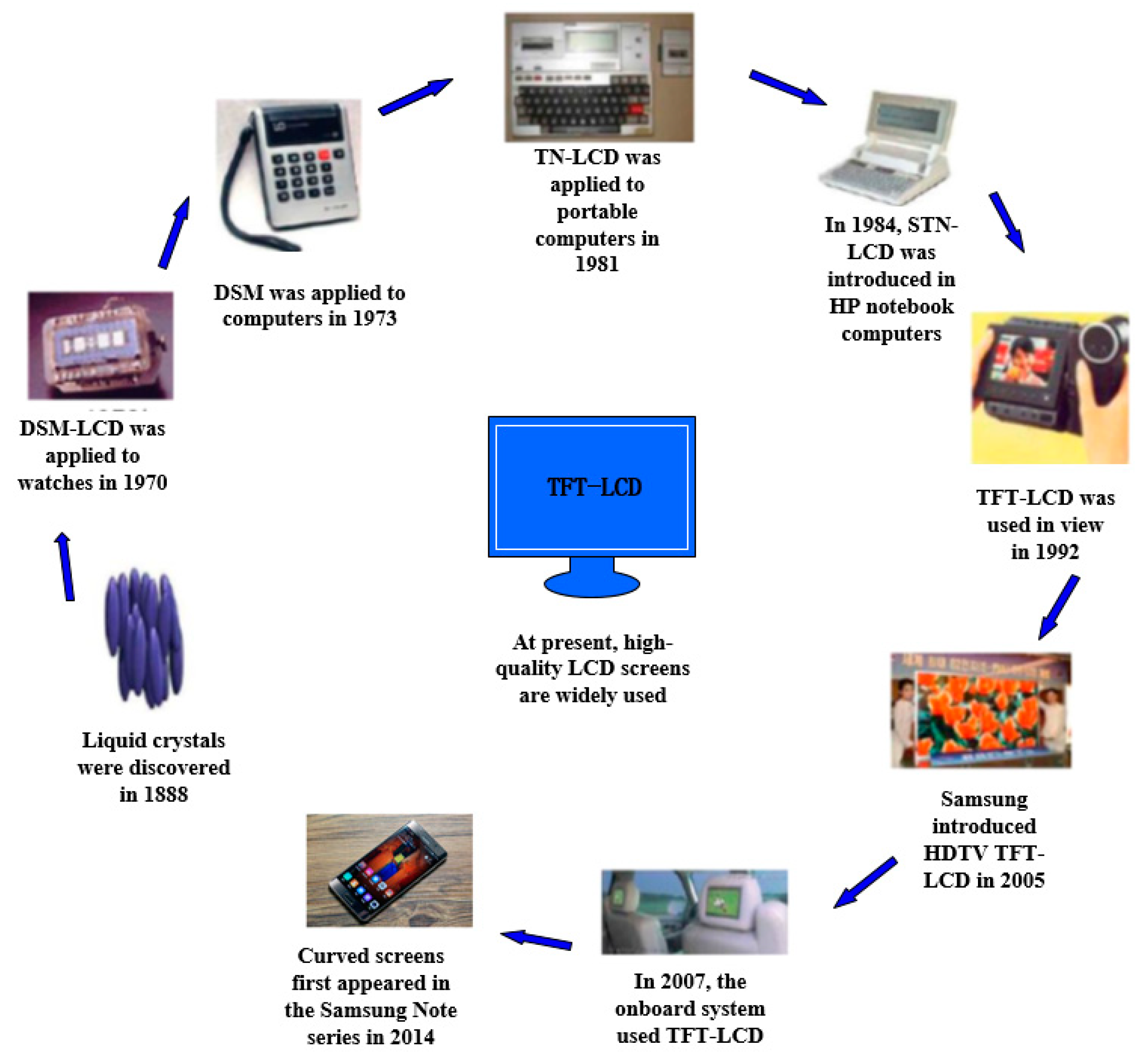
wave and particle behaviors of lcd displays brands

The theoretical sketch of the wave-particle scheme for the single photon is displayed in Fig. 1. A photon is initially prepared in a polarization state \(\left| {{\psi _0}} \right\rangle = {\rm{cos}}\,\alpha \left| {\rm V} \right\rangle + {\rm{sin}}\,\alpha \left| {\rm{H}} \right\rangle\), where \(\left| {\rm V} \right\rangle\) and \(\left| {\rm{H}} \right\rangle\) are the vertical and horizontal polarization states and α is adjustable by a preparation half-wave plate (not shown in the figure). After crossing the preparation part of the setup of Fig. 1 (see Supplementary Notes 1 and 2 and Supplementary Fig. 1 for details), the photon state is

$$\left| {{\psi _{\rm{f}}}} \right\rangle = {\rm{cos}}\,\alpha \left| {{\rm{wave}}} \right\rangle + {\rm{sin}}\,\alpha \left| {{\rm{particle}}} \right\rangle ,$$

$$\begin{array}{*{20}{l}}\\ {\left| {{\rm{wave}}} \right\rangle } = {{e^{i{\phi _1}/2}}\left( {{\rm{cos}}\frac{{{\phi _1}}}{2}\left| 1 \right\rangle - i\,{\rm{sin}}\frac{{{\phi _1}}}{2}\left| 3 \right\rangle } \right),} \hfill \\ {\left| {{\rm{particle}}} \right\rangle } = {\frac{1}{{\sqrt 2 }}\left( {\left| 2 \right\rangle + {e^{i{\phi _2}}}\left| 4 \right\rangle } \right),} \hfill \\ \end{array}$$

operationally represent the capacity \(\left( {\left| {{\rm{wave}}} \right\rangle } \right)\) and incapacity \(\left( {\left| {{\rm{particle}}} \right\rangle } \right)\) of the photon to produce interference\(\left| {{\rm{wave}}} \right\rangle\) state the probability of detecting the photon in the path \(\left| n \right\rangle \,\) (n = 1, 3) depends on the phase ϕ

1: the photon must have traveled along both paths simultaneously (see upper MZI in Fig. 1), revealing its wave behavior. Instead, for the \(\left| {{\rm{particle}}} \right\rangle\) state the probability to detect the photon in the path \(\left| n \right\rangle \,\) (n = 2, 4) is 1/2, regardless of phase ϕ

2: thus, the photon must have crossed only one of the two paths (see lower MZI of Fig. 1), showing its particle behavior. Notice that the scheme is designed in such a way that \(\left| {\rm V} \right\rangle\)

Conceptual figure of the wave-particle toolbox. A single photon is coherently separated in two spatial modes by means of a polarizing beam-splitter (PBS) according to its initial polarization state (in). A half-wave plate (HWP) is placed after the PBS to obtain equal polarizations between the two modes. One mode is injected in a complete Mach-Zehnder interferometer (MZI) with phase ϕ

1, thus exhibiting wave-like behavior. The second mode is injected in a Mach-Zehnder interferometer lacking the second beam-splitter, thus exhibiting particle-like behavior (no dependence on ϕ

To verify the coherent wave-particle superposition as a function of the parameter α, the wave and particle states have to interfere at the detection level. This goal is achieved by exploiting two symmetric beam-splitters where the output paths (modes) are recombined, as illustrated in the detection part of Fig. 1. The probability P

We remark that the terms \({{\cal I}_{\rm{c}}}\), \({{\cal I}_{\rm{s}}}\) in the detection probabilities exclusively stem from the interference between the \(\left| {{\rm{wave}}} \right\rangle\) and \(\left| {{\rm{particle}}} \right\rangle\) components appearing in the generated superposition state \(\left| {{\psi _{\rm{f}}}} \right\rangle\) of Eq. (1). This fact is further evidenced by the appearance, in these interference terms, of the factor \({\cal C} = {\rm{sin}}\,2\alpha\), which is the amount of quantum coherence owned by \(\left| {{\psi _{\rm{f}}}} \right\rangle\) in the basis {\(\left| {{\rm{wave}}} \right\rangle\), \(\left| {{\rm{particle}}} \right\rangle\)} theoretically quantified according to the standard l

1-norm\({{\cal I}_{\rm{c}}}\), \({{\cal I}_{\rm{s}}}\) are always identically zero (independently of phase values) when the final state of the photon is: (i) \(\left| {{\rm{wave}}} \right\rangle\) (α = 0); (ii) \(\left| {{\rm{particle}}} \right\rangle\) (α = π/2); (iii) a classical incoherent mixture \({\rho _{\rm{f}}} = {\rm{co}}{{\rm{s}}^2}\alpha \left| {{\rm{wave}}} \right\rangle \left\langle {{\rm{wave}}} \right| + {\rm{si}}{{\rm{n}}^2}\alpha \left| {{\rm{particle}}} \right\rangle \left\langle {{\rm{particle}}} \right|\) (which can be theoretically produced by the same scheme starting from an initial mixed polarization state of the photon).

The experimental single-photon toolbox, realizing the proposed scheme of Fig. 1, is displayed in Fig. 2 (see Methods for more details). The implemented layout presents the advantage of being interferometrically stable, thus not requiring active phase stabilization between the modes. Figure 3 shows the experimental results for the measured single-photon probabilities P

n. For α = 0, the photon is vertically polarized and entirely reflected from the PBS to travel along path 1, then split at BS1 into two paths, both leading to the same BS3 which allows these two paths to interfere with each other before detection. The photon detection probability at each detector Dn (n = 1, 2, 3, 4) depends on the phase shift ϕ

1: \({P_1}\left( {\alpha = 0} \right) = {P_2}\left( {\alpha = 0} \right) = \frac{1}{2}{\rm{co}}{{\rm{s}}^2}\frac{{{\phi _1}}}{2}\), \({P_3}\left( {\alpha = 0} \right) = {P_4}\left( {\alpha = 0} \right) = \frac{1}{2}{\rm{si}}{{\rm{n}}^2}\frac{{{\phi _1}}}{2}\), as expected from Eqs. (3) and (4). After many such runs an interference pattern emerges, exhibiting the wave-like nature of the photon. Differently, if initially α = π/2, the photon is horizontally polarized and, as a whole, transmitted by the PBS to path 2, then split at BS2 into two paths (leading, respectively, to BS4 and BS5) which do not interfere anywhere. Hence, the phase shift ϕ

2 plays no role on the photon detection probability and each detector has an equal chance to click: \({P_1}\left( {\alpha = \frac{\pi }{2}} \right) = {P_2}\left( {\alpha = \frac{\pi }{2}} \right) = {P_3}\left( {\alpha = \frac{\pi }{2}} \right) = {P_4}\left( {\alpha = \frac{\pi }{2}} \right) = \frac{1}{4}\), as predicted by Eqs. (3) and (4), showing particle-like behavior without any interference pattern. Interestingly, for 0 < α < π/2, the photon simultaneously behaves like wave and particle. The coherent continuous morphing transition from wave to particle behavior as α varies from 0 to π/2 is clearly seen from Fig. 4a and contrasted with the morphing observed for a mixed incoherent wave-particle state ρ

2 = 0, the coherence of the generated state is also directly quantified by measuring the expectation value of an observable \(\sigma _x^{1234}\), defined in the four-dimensional basis of the photon paths \(\left\{ {\left| 1 \right\rangle ,\left| 2 \right\rangle ,\left| 3 \right\rangle ,\left| 4 \right\rangle } \right\}\) of the preparation part of the setup as a Pauli matrix σ

x between modes (1, 2) and between modes (3, 4). It is then possible to straightforwardly show that \(\left\langle {\sigma _x^{1234}} \right\rangle = {\rm{Tr}}\left( {\sigma _x^{1234}{\rho _{\rm{f}}}} \right) = 0\) for any incoherent state ρ

f, while \(\sqrt 2 \left\langle {\sigma _x^{1234}} \right\rangle = {\rm{sin}}\,2\alpha = {\cal C}\) for an arbitrary state of the form \(\left| {{\psi _{\rm{f}}}} \right\rangle\) defined in Eq. (1). Insertion of beam-splitters BS4 and BS5 in the detection part of the setup (corresponding to β = 22.5° in the output wave-plate of Fig. 2) rotates the initial basis \(\left\{ {\left| 1 \right\rangle ,\left| 2 \right\rangle ,\left| 3 \right\rangle ,\left| 4 \right\rangle } \right\}\) generating a measurement basis of eigenstates of \(\sigma _x^{1234}\), whose expectation value is thus obtained in terms of the detection probabilities as \(\left\langle {\sigma _x^{1234}} \right\rangle = {P_1} - {P_2} + {P_3} - {P_4}\) (see Supplementary Note 2). As shown in Fig. 4c, d, the observed behavior of \(\sqrt 2 \left\langle {\sigma _x^{1234}} \right\rangle\) as a function of α confirms the theoretical predictions for both coherent \(\left| {{\psi _{\rm{f}}}} \right\rangle\) (Fig. 4c) and mixed (incoherent) ρ

f wave-particle states (the latter being obtained in the experiment by adding a relative time delay in the interferometer paths larger than the photon coherence time to lose quantum interference, Fig. 4d).

Experimental setup for wave-particle states. a Overview of the apparatus for the generation of single-photon wave-particle superposition. An heralded single-photon is prepared in an arbitrary linear polarization state through a half-wave plate rotated at an angle α/2 and injected into the wave-particle toolbox. b Overview of the apparatus for the generation of a two-photon wave-particle entangled state. Each photon of a polarization entangled state is injected into an independent wave-particle toolbox to prepare the output state. c Actual implemented wave-particle toolbox, reproducing the action of the scheme shown in Fig. 1. Top subpanel: top view of the scheme, where red and purple lines represent optical paths lying in two vertical planes. Bottom subpanel: 3-d scheme of the apparatus. The interferometer is composed of beam-displacing prisms (BDP), half-wave plates (HWP), and liquid crystal devices (LC), the latter changing the phases ϕ

2. The output modes are finally separated by means of a polarizing beam-splitter (PBS). The scheme corresponds to the presence of BS4 and BS5 in Fig. 1 for β = 22.5°, while setting β = 0 equals to the absence of BS4 and BS5. The same color code for the optical elements (reported in the figure legend) is employed for the top view and for the 3-d view of the apparatus. d Picture of the experimental apparatus. The green frame highlights the wave-particle toolbox

1, for different values of α. a Wave behavior (α = 0). b Particle behavior (α = π/2). c Coherent wave-particle superposition (α = π/4). d Incoherent mixture of wave and particle behaviors (α = π/4). Points: experimental data. Dashed curves: best-fit of the experimental data. Color legend: orange (P1), green (P2), purple (P3), blue (P

1 and of the angle α. Points: experimental data. Surfaces: theoretical expectations. In all plots, error bars are standard deviation due to the Poissonian statistics of single-photon counting

4). In a black triangles highlighted the position for wave behavior (α = 0), black circle for particle behavior (α = π/2) and black diamonds highlight the position for coherent wave-particle superposition behavior (α = π/4). c Coherence measure \(\sqrt 2 \left\langle {\sigma _x^{1234}} \right\rangle\) as a function of α in the coherent case and d for an incoherent mixture (the latter showing no dependence on α). Points: experimental data. Solid curves: theoretical expectations. Error bars are standard deviations due to the Poissonian statistics of single-photon counting

The above single-photon scheme constitutes the basic toolbox which can be extended to create a wave-particle entangled state of two photons, as shown in Fig. 2b. Initially, a two-photon polarization maximally entangled state \({\left| \Psi \right\rangle _{{\rm{AB}}}} = \frac{1}{{\sqrt 2 }}\left( {\left| {{\rm VV}} \right\rangle + \left| {{\rm{HH}}} \right\rangle } \right)\) is prepared (the procedure works in general for arbitrary weights, see Supplementary Note 3). Each photon is then sent to one of two identical wave-particle toolboxes which provide the final state

$${\left| \Phi \right\rangle _{{\rm{AB}}}} = \frac{1}{{\sqrt 2 }}\left( {\left| {{\rm{wave}}} \right\rangle \left| {{\rm{wave}"}} \right\rangle + \left| {{\rm{particle}}} \right\rangle \left| {{\rm{particle}"}} \right\rangle } \right),$$

where the single-photon states \(\left| {{\rm{wave}}} \right\rangle\), \(\left| {{\rm{particle}}} \right\rangle\), \(\left| {{\rm{wave}"}} \right\rangle\), \(\left| {{\rm{particle}"}} \right\rangle\) are defined in Eq. (2), with parameters and paths related to the corresponding wave-particle toolbox. Using the standard concurrenceC to quantify the amount of entanglement of this state in the two-photon wave-particle basis, one immediately finds C = 1. The generated state \({\left| \Phi \right\rangle _{{\rm{AB}}}}\) is thus a wave-particle maximally entangled state (Bell state) of two photons in separated locations.

The output two-photon state is measured after the two toolboxes. The results are shown in Fig. 5. Coincidences between the four outputs of each toolbox are measured by varying ϕ

1 and \(\phi _1^{\prime}\). The first set of measurements (Fig. 5a–d) is performed by setting the angles of the output wave-plates (see Fig. 2c) at {β = 0, β′ = 0}, corresponding to removing both BS4 and BS5 in Fig. 1 (absence of interference between single-photon wave and particle states). In this case, detectors placed at outputs (1, 3) and (1′, 3′) reveal wave-like behavior, while detectors placed at outputs (2, 4) and (2′, 4′) evidence a particle-like one. As expected, the two-photon probabilities \({P_{n{n^{\prime}}}}\) for the particle detectors remain unchanged while varying ϕ

1 and \(\phi _1^{\prime}\), whereas the \({P_{nn"}}\) for the wave detectors show interference fringes. Moreover, no contribution of crossed wave-particle coincidences \({P_{nn"}}\) is obtained, due to the form of the entangled state. The second set of measurements (Fig. 5e–h) is performed by setting the angles of the output wave-plates at {β = 22.5°, β′ = 22.5°}, corresponding to the presence of BS4 and BS5 in Fig. 1 (the presence of interference between single-photon wave and particle states). We now observe nonzero contributions across all the probabilities depending on the specific settings of phases ϕ

1 and \(\phi _1^{\prime}\). The presence of entanglement in the wave-particle behavior is also assessed by measuring the quantity \({\cal E} = {P_{22"}} - {P_{21"}}\) as a function of ϕ

1, with fixed \(\phi _1^{\prime} = {\phi _2} = \phi _2^{\prime} = 0\). According to the general expressions of the coincidence probabilities (see Supplementary Note 3), \({\cal E}\) is proportional to the concurrence C and identically zero (independently of phase values) if and only if the wave-particle two-photon state is separable (e.g., \(\left| {{\rm{wave}}} \right\rangle\) ⊗ \(\left| {{\rm{wave}"}} \right\rangle\) or a maximal mixture of two-photon wave and particle states). For \(\left| \Phi \right\rangle\)

AB of Eq. (5) the theoretical prediction is \({\cal E} = \left( {1{\rm{/}}4} \right){\rm{co}}{{\rm{s}}^{\rm{2}}}\left( {{\phi _1}{\rm{/}}2} \right)\), which is confirmed by the results reported in Fig. 5i, j (within the reduction due to visibility). A further test of the generated wave-particle entanglement is finally performed by the direct measure of the expectation values \(\left\langle {\cal W} \right\rangle = {\rm{Tr}}\left( {{\cal W}\rho } \right)\) of a suitable entanglement witness

z Pauli matrix between modes (1, 2) and between modes (3, 4). The measurement basis of \(\sigma _z^{1234}\) is that of the initial paths \(\left\{ {\left| 1 \right\rangle ,\left| 2 \right\rangle ,\left| 3 \right\rangle ,\left| 4 \right\rangle } \right\}\) exiting the preparation part of the single-photon toolbox. It is possible to show that \({\rm{Tr}}\left( {{\cal W}{\rho _{\rm{s}}}} \right) \ge 0\) for any two-photon separable state ρ

e is entangled in the photons wave-particle behavior (see Supplementary Note 3). The expectation values of \({\cal W}\) measured in the experiment in terms of the 16 coincidence probabilities P

1 = 0, \(\phi _1^\prime\) = π). These observations altogether prove the existence of quantum correlations between wave and particle states of two photons in the entangled state \(\left| \Phi \right\rangle\)

Generation of wave-particle entangled superposition with a two-photon state. Measurements of the output coincidence probabilities \({P_{nn"}}\) to detect one photon in output mode n of the first toolbox and one in the output mode n′ of the second toolbox, with different phases ϕ

1 = π and \(\phi _1^{\prime} = \pi\). White bars: theoretical predictions. Colored bars: experimental data. Orange bars: \({P_{n{n^{\prime}}}}\) contributions for detectors Dn and \({{\rm{D}}_{n"}}\) linked to wave-like behavior for both photons (in the absence of BS4 and BS5). Cyan bars: \({P_{nn"}}\) contributions for detectors Dn and \({{\rm{D}}_{n"}}\) linked to particle-like behavior for both photons (in the absence of BS4 and BS5). Magenta bars: \({P_{nn"}}\) contributions for detectors Dn and \({{\rm{D}}_{n"}}\) linked to wave-like behavior for one photon and particle-like behavior for the other one (in absence of BS4 and BS5). Darker regions in colored bars correspond to 1 σ error interval, due to the Poissonian statistics of two-photon coincidences. i, j, Quantitative verification of wave-particle entanglement. i, \({P_{22"}}\) (blue) and \({P_{21"}}\) (green) and j, \({\cal E} = {P_{22"}} - {P_{21"}}\), as a function of ϕ

1 for \(\phi _1^{\prime} = 0\) and {β = 22.5°, β′ = 22.5°}. Error bars are standard deviations due to the Poissonian statistics of two-photon coincidences. Dashed curves: best-fit of the experimental data

Just what is the true nature of light? Is it a wave or perhaps a flow of extremely small particles? These questions have long puzzled scientists. Let"s travel through history as we study the matter.

Around 1700, Newton concluded that light was a group of particles (corpuscular theory). Around the same time, there were other scholars who thought that light might instead be a wave (wave theory). Light travels in a straight line, and therefore it was only natural for Newton to think of it as extremely small particles that are emitted by a light source and reflected by objects. The corpuscular theory, however, cannot explain wave-like light phenomena such as diffraction and interference. On the other hand, the wave theory cannot clarify why photons fly out of metal that is exposed to light (the phenomenon is called the photoelectric effect, which was discovered at the end of the 19th century). In this manner, the great physicists have continued to debate and demonstrate the true nature of light over the centuries.

Known for his Law of Universal Gravitation, English physicist Sir Isaac Newton (1643 to 1727) realized that light had frequency-like properties when he used a prism to split sunlight into its component colors. Nevertheless, he thought that light was a particle because the periphery of the shadows it created was extremely sharp and clear.

The wave theory, which maintains that light is a wave, was proposed around the same time as Newton"s theory. In 1665, Italian physicist Francesco Maria Grimaldi (1618 to 1663) discovered the phenomenon of light diffraction and pointed out that it resembles the behavior of waves. Then, in 1678, Dutch physicist Christian Huygens (1629 to 1695) established the wave theory of light and announced the Huygens" principle.

Some 100 years after the time of Newton, French physicist Augustin-Jean Fresnel (1788 to 1827) asserted that light waves have an extremely short wavelength and mathematically proved light interference. In 1815, he devised physical laws for light reflection and refraction, as well. He also hypothesized that space is filled with a medium known as ether because waves need something that can transmit them. In 1817, English physicist Thomas Young (1773 to 1829) calculated light"s wavelength from an interference pattern, thereby not only figuring out that the wavelength is 1 μm ( 1 μm = one millionth of a meter ) or less, but also having a handle on the truth that light is a transverse wave. At that point, the particle theory of light fell out of favor and was replaced by the wave theory.

The next theory was provided by the brilliant Scottish physicist James Clerk Maxwell (1831 to 1879). In 1864, he predicted the existence of electromagnetic waves, the existence of which had not been confirmed before that time, and out of his prediction came the concept of light being a wave, or more specifically, a type of electromagnetic wave. Until that time, the magnetic field produced by magnets and electric currents and the electric field generated between two parallel metal plates connected to a charged capacitor were considered to be unrelated to one another. Maxwell changed this thinking when, in 1861, he presented Maxwell"s equations: four equations for electromagnetic theory that shows magnetic fields and electric fields are inextricably linked. This led to the introduction of the concept of electromagnetic waves other than visible light into light research, which had previously focused only on visible light.

The term electromagnetic wave tends to bring to mind the waves emitted from cellular telephones, but electromagnetic waves are actually waves produced by electricity and magnetism. Electromagnetic waves always occur wherever electricity is flowing or radio waves are flying about. Maxwell"s equations, which clearly revealed the existence of such electromagnetic waves, were announced in 1861, becoming the most fundamental law of electromagnetics. These equations are not easy to understand, but let"s take an in-depth look because they concern the true nature of light.

Maxwell"s four equations have become the most fundamental law in electromagnetics. The first equation formulates Faraday"s Law of Electromagnetic Induction, which states that changing magnetic fields generate electrical fields, producing electrical current.

The second equation is called the Ampere-Maxwell Law. It adds to Ampere"s Law, which states an electric current flowing over a wire produces a magnetic field around itself, and another law that says a changing magnetic field also gives rise to a property similar to an electric current (a displacement current), and this too creates a magnetic field around itself. The term displacement current actually is a crucial point.

The fourth equation is Gauss"s Law of magnetic field, stating a magnetic field has no source (magnetic monopole) equivalent to that of an electric charge.

If you take two parallel metal plates (electrodes) and connect one to the positive pole and the other to the negative pole of a battery, you will create a capacitor. Direct-current (DC) electricity will simply collect between the two metal plates, and no current will flow between them. However, if you connect alternating current (AC) that changes drastically, electric current will start to flow along the two electrodes. Electric current is a flow of electrons, but between these two electrodes there is nothing but space, and thus electrons do not flow.

Maxell wondered what this could mean. Then it came to him that applying an AC voltage to the electrodes generates a changing electric field in the space between them, and this changing electric field acts as a changing electric current. This electric current is what we mean when we use the term displacement current.

A most unexpected conclusion can be drawn from the idea of a displacement current. In short, electromagnetic waves can exist. This also led to the discovery that in space there are not only objects that we can see with our eyes, but also intangible fields that we cannot see. The existence of fields was revealed for the first time. Solving Maxwell"s equations reveals the wave equation, and the solution for that equation results in a wave system in which electric fields and magnetic fields give rise to each other while traveling through space.

The form of electromagnetic waves was expressed in a mathematical formula. Magnetic fields and electric fields are inextricably linked, and there is also an entity called an electromagnetic field that is solely responsible for bringing them into existence.

Now let"s take a look at a capacitor. Applying AC voltage between two metal electrodes produces a changing electric field in space, and this electric field in turn creates a displacement current, causing an electric current to flow between the electrodes. At the same time, the displacement current produces a changing magnetic field around itself according to the second of Maxwell"s equations (Ampere-Maxwell Law).

The resulting magnetic field creates an electric field around itself according to the first of Maxwell"s equations (Faraday"s Law of Electromagnetic Induction). Based on the fact that a changing electric field creates a magnetic field in this manner, electromagnetic waves-in which an electric field and magnetic field alternately appear-are created in the space between the two electrodes and travel into their surroundings. Antennas that emit electromagnetic waves are created by harnessing this principle.

Maxwell calculated the speed of travel for the waves, i.e. electromagnetic waves, revealed by his mathematical formulas. He said speed was simply one over the square root of the electric permittivity in vacuum times the magnetic permeability in vacuum. When he assigned "9 x 109/4π for the electric permittivity in vacuum" and "4π x 10-7 for the magnetic permeability in vacuum," both of which were known values at the time, his calculation yielded 2.998 x 108 m/sec. This exactly matched the previously discovered speed of light. This led Maxwell to confidently state that light is a type of electromagnetic wave.

The theory of light being a particle completely vanished until the end of the 19th century when Albert Einstein revived it. Now that the dual nature of light as "both a particle and a wave" has been proved, its essential theory was further evolved from electromagnetics into quantum mechanics. Einstein believed light is a particle (photon) and the flow of photons is a wave. The main point of Einstein"s light quantum theory is that light"s energy is related to its oscillation frequency. He maintained that photons have energy equal to "Planck"s constant times oscillation frequency," and this photon energy is the height of the oscillation frequency while the intensity of light is the quantity of photons. The various properties of light, which is a type of electromagnetic wave, are due to the behavior of extremely small particles called photons that are invisible to the naked eye.

The German physicist Albert Einstein (1879 to 1955), famous for his theories of relativity, conducted research on the photoelectric effect, in which electrons fly out of a metal surface exposed to light. The strange thing about the photoelectric effect is the energy of the electrons (photoelectrons) that fly out of the metal does not change whether the light is weak or strong. (If light were a wave, strong light should cause photoelectrons to fly out with great power.) Another puzzling matter is how photoelectrons multiply when strong light is applied. Einstein explained the photoelectric effect by saying that "light itself is a particle," and for this he received the Nobel Prize in Physics.

The light particle conceived by Einstein is called a photon. The main point of his light quantum theory is the idea that light"s energy is related to its oscillation frequency (known as frequency in the case of radio waves). Oscillation frequency is equal to the speed of light divided by its wavelength. Photons have energy equal to their oscillation frequency times Planck"s constant. Einstein speculated that when electrons within matter collide with photons, the former takes the latter"s energy and flies out, and that the higher the oscillation frequency of the photons that strike, the greater the electron energy that will come flying out.

In short, he was saying that light is a flow of photons, the energy of these photons is the height of their oscillation frequency, and the intensity of the light is the quantity of its photons.

Einstein proved his theory by proving that the Planck"s constant he derived based on his experiments on the photoelectric effect exactly matched the constant 6.6260755 x 10-34 (Planck"s constant) that German physicist Max Planck (1858 to 1947) obtained in 1900 through his research on electromagnetic waves. This too pointed to an intimate relationship between the properties and oscillation frequency of light as a wave and the properties and momentum (energy) of light as a particle, or in other words, the dual nature of light as both a particle and a wave.

French theoretical physicist Louis de Broglie (1892 to 1987) furthered such research on the wave nature of particles by proving that there are particles (electrons, protons and neutrons) besides photons that have the properties of a wave. According to de Broglie, all particles traveling at speeds near that of light adopt the properties and wavelength of a wave in addition to the properties and momentum of a particle. He also derived the relationship "wavelength x momentum = Planck"s constant."

From another perspective, one could say that the essence of the dual nature of light as both a particle and a wave could already be found in Planck"s constant. The evolution of this idea is contributing to diverse scientific and technological advances, including the development of electron microscopes.

Quantum dots (QDs) are semiconductor particles a few nanometres in size, having optical and electronic properties that differ from those of larger particles as a result of quantum mechanics. They are a central topic in nanotechnology. When the quantum dots are illuminated by UV light, an electron in the quantum dot can be excited to a state of higher energy. In the case of a semiconducting quantum dot, this process corresponds to the transition of an electron from the valence band to the conductance band. The excited electron can drop back into the valence band releasing its energy as light. This light emission (photoluminescence) is illustrated in the figure on the right. The color of that light depends on the energy difference between the conductance band and the valence band, or the transition between discrete energy states when band structure is no longer a good definition in QDs.

In the language of materials science, nanoscale semiconductor materials tightly confine either electrons or electron holes. Quantum dots are sometimes referred to as artificial atoms, emphasizing their singularity, having bound, discrete electronic states, like naturally occurring atoms or molecules.wave functions in quantum dots resemble the ones in real atoms.artificial molecule can be made, exhibiting hybridization even at room temperature.

Quantum dots have properties intermediate between bulk semiconductors and discrete atoms or molecules. Their optoelectronic properties change as a function of both size and shape.wavelengths, with colors such as orange, or red. Smaller QDs (2–3 nm) emit shorter wavelengths, yielding colors like blue, and green. However, the specific colors vary depending on the exact composition of the QD.

Potential applications of quantum dots include single-electron transistors, solar cells, LEDs, lasers,single-photon sources,second-harmonic generation, quantum computing,microscopy,medical imaging.inkjet printing, and spin-coating.Langmuir-Blodgett thin-films.semiconductor fabrication.

Colloidal semiconductor nanocrystals are synthesized from solutions, much like traditional chemical processes. The main difference is the product neither precipitates as a bulk solid nor remains dissolved.precursors decompose forming monomers which then nucleate and generate nanocrystals. Temperature is a critical factor in determining optimal conditions for the nanocrystal growth. It must be high enough to allow for rearrangement and annealing of atoms during the synthesis process while being low enough to promote crystal growth. The concentration of monomers is another critical factor that has to be stringently controlled during nanocrystal growth. The growth process of nanocrystals can occur in two different regimes, "focusing" and "defocusing". At high monomer concentrations, the critical size (the size where nanocrystals neither grow nor shrink) is relatively small, resulting in growth of nearly all particles. In this regime, smaller particles grow faster than large ones (since larger crystals need more atoms to grow than small crystals) resulting in the size distribution focusing, yielding an improbable distribution of nearly monodispersed particles. The size focusing is optimal when the monomer concentration is kept such that the average nanocrystal size present is always slightly larger than the critical size. Over time, the monomer concentration diminishes, the critical size becomes larger than the average size present, and the distribution defocuses.

There are colloidal methods to produce many different semiconductors. Typical dots are made of binary compounds such as lead sulfide, lead selenide, cadmium selenide, cadmium sulfide, cadmium telluride, indium arsenide, and indium phosphide. Dots may also be made from ternary compounds such as cadmium selenide sulfide. Further, recent advances have been made which allow for synthesis of colloidal perovskite quantum dots.nanometers, and at 10 nm in diameter, nearly 3 million quantum dots could be lined up end to end and fit within the width of a human thumb.

Idealized image of colloidal nanoparticle of lead sulfide (selenide) with complete passivation by oleic acid, oleyl amine and hydroxyl ligands (size ≈5nm)

Large batches of quantum dots may be synthesized via colloidal synthesis. Due to this scalability and the convenience of benchtop conditions, colloidal synthetic methods are promising for commercial applications.

Plasma synthesis has evolved to be one of the most popular gas-phase approaches for the production of quantum dots, especially those with covalent bonds.silicon (Si) and germanium (Ge) quantum dots have been synthesized by using nonthermal plasma. The size, shape, surface and composition of quantum dots can all be controlled in nonthermal plasma.

Self-assembled quantum dots are typically between 5 and 50 nm in size. Quantum dots defined by lithographically patterned gate electrodes, or by etching on two-dimensional electron gases in semiconductor heterostructures can have lateral dimensions between 20 and 100 nm.

Some quantum dots are small regions of one material buried in another with a larger band gap. These can be so-called core–shell structures, e.g., with CdSe in the core and ZnS in the shell, or from special forms of silica called ormosil. Sub-monolayer shells can also be effective ways of passivating the quantum dots, such as PbS cores with sub-monolayer CdS shells.

Self-assembled quantum dots nucleate spontaneously under certain conditions during molecular beam epitaxy (MBE) and metalorganic vapour-phase epitaxy (MOVPE), when a material is grown on a substrate to which it is not lattice matched. The resulting strain leads to the formation of islands on top of a two-dimensional wetting layer. This growth mode is known as Stranski–Krastanov growth.indium gallium arsenide (InGaAs) quantum dots in gallium arsenide (GaAs).quantum cryptography (i.e. single photon sources) and quantum computation. The main limitations of this method are the cost of fabrication and the lack of control over positioning of individual dots.

Individual quantum dots can be created from two-dimensional electron or hole gases present in remotely doped quantum wells or semiconductor heterostructures called lateral quantum dots. The sample surface is coated with a thin layer of resist. A lateral pattern is then defined in the resist by electron beam lithography. This pattern can then be transferred to the electron or hole gas by etching, or by depositing metal electrodes (lift-off process) that allow the application of external voltages between the electron gas and the electrodes. Such quantum dots are mainly of interest for experiments and applications involving electron or hole transport, i.e., an electrical current.

The energy spectrum of a quantum dot can be engineered by controlling the geometrical size, shape, and the strength of the confinement potential. Also, in contrast to atoms, it is relatively easy to connect quantum dots by tunnel barriers to conducting leads, which allows the application of the techniques of tunneling spectroscopy for their investigation.

The quantum dot absorption features correspond to transitions between discrete, three-dimensional particle in a box states of the electron and the hole, both confined to the same nanometer-size box. These discrete transitions are reminiscent of atomic spectra and have resulted in quantum dots also being called

Complementary metal-oxide-semiconductor (CMOS) technology can be employed to fabricate silicon quantum dots. Ultra small (L=20 nm, W=20 nm) CMOS transistors behave as single electron quantum dots when operated at cryogenic temperature over a range of −269 °C (4 K) to about −258 °C (15 K). The transistor displays Coulomb blockade due to progressive charging of electrons (holes) one by one. The number of electrons (holes) confined in the channel is driven by the gate voltage, starting from an occupation of zero electrons (holes), and it can be set to 1 or many.

Genetically engineered M13 bacteriophage viruses allow preparation of quantum dot biocomposite structures.semiconductor surfaces through the method of selection by combinatorial phage display.liquid crystalline structures of wild-type viruses (Fd, M13, and TMV) are adjustable by controlling the solution concentrations, solution ionic strength, and the external magnetic field applied to the solutions. Consequently, the specific recognition properties of the virus can be used to organize inorganic nanocrystals, forming ordered arrays over the length scale defined by liquid crystal formation. Using this information, Lee et al. (2000) were able to create self-assembled, highly oriented, self-supporting films from a phage and ZnS precursor solution. This system allowed them to vary both the length of bacteriophage and the type of inorganic material through genetic modification and selection.

Highly ordered arrays of quantum dots may also be self-assembled by electrochemical techniques. A template is created by causing an ionic reaction at an electrolyte-metal interface which results in the spontaneous assembly of nanostructures, including quantum dots, onto the metal which is then used as a mask for mesa-etching these nanostructures on a chosen substrate.

Quantum dot manufacturing relies on a process called high temperature dual injection which has been scaled by multiple companies for commercial applications that require large quantities (hundreds of kilograms to tonnes) of quantum dots. This reproducible production method can be applied to a wide range of quantum dot sizes and compositions.

The bonding in certain cadmium-free quantum dots, such as III-V-based quantum dots, is more covalent than that in II-VI materials, therefore it is more difficult to separate nanoparticle nucleation and growth via a high temperature dual injection synthesis. An alternative method of quantum dot synthesis, the molecular seeding process, provides a reproducible route to the production of high-quality quantum dots in large volumes. The process utilises identical molecules of a molecular cluster compound as the nucleation sites for nanoparticle growth, thus avoiding the need for a high temperature injection step. Particle growth is maintained by the periodic addition of precursors at moderate temperatures until the desired particle size is reached.

Another approach for the mass production of colloidal quantum dots can be seen in the transfer of the well-known hot-injection methodology for the synthesis to a technical continuous flow system. The batch-to-batch variations arising from the needs during the mentioned methodology can be overcome by utilizing technical components for mixing and growth as well as transport and temperature adjustments. For the production of CdSe based semiconductor nanoparticles this method has been investigated and tuned to production amounts of kg per month. Since the use of technical components allows for easy interchange in regards of maximum throughput and size, it can be further enhanced to tens or even hundreds of kilograms.

In 2011 a consortium of U.S. and Dutch companies reported a milestone in high volume quantum dot manufacturing by applying the traditional high temperature dual injection method to a flow system.

On 23 January 2013 Dow entered into an exclusive licensing agreement with UK-based Nanoco for the use of their low-temperature molecular seeding method for bulk manufacture of cadmium-free quantum dots for electronic displays, and on 24 September 2014 Dow commenced work on the production facility in South Korea capable of producing sufficient quantum dots for "millions of cadmium-free televisions and other devices, such as tablets". Mass production is due to commence in mid-2015.

In many regions of the world there is now a restriction or ban on the use of heavy metals in many household goods, which means that most cadmium-based quantum dots are unusable for consumer-goods applications.

For commercial viability, a range of restricted, heavy-metal-free quantum dots has been developed showing bright emissions in the visible and near-infrared region of the spectrum and have similar optical properties to those of CdSe quantum dots. Among these materials are InP/ZnS, CuInS/ZnS, Si, Ge and C.

Some quantum dots pose risks to human health and the environment under certain conditions.cadmium and have yet to be demonstrated in animal models after physiologically relevant dosing.In vitro studies, based on cell cultures, on quantum dots (QD) toxicity suggest that their toxicity may derive from multiple factors including their physicochemical characteristics (size, shape, composition, surface functional groups, and surface charges) and their environment. Assessing their potential toxicity is complex as these factors include properties such as QD size, charge, concentration, chemical composition, capping ligands, and also on their oxidative, mechanical and photolytic stability.

Many studies have focused on the mechanism of QD cytotoxicity using model cell cultures. It has been demonstrated that after exposure to ultraviolet radiation or oxidation by air, CdSe QDs release free cadmium ions causing cell death.reactive oxygen species after exposure to light, which in turn can damage cellular components such as proteins, lipids and DNA.

Although concentration of QDs in certain organelles have been reported in in vivo studies using animal models, no alterations in animal behavior, weight, hematological markers or organ damage has been found through either histological or biochemical analysis.Tc.exocytosis of QDs is still poorly studied in the literature.

While significant research efforts have broadened the understanding of toxicity of QDs, there are large discrepancies in the literature, and questions still remain to be answered. Diversity of this class of material as compared to normal chemical substances makes the assessment of their toxicity very challenging. As their toxicity may also be dynamic depending on the environmental factors such as pH level, light exposure and cell type, traditional methods of assessing toxicity of chemicals such as LD50 are not applicable for QDs. Therefore, researchers are focusing on introducing novel approaches and adapting existing methods to include this unique class of materials.carbon quantum dots, a new generation of optically-active nanoparticles potentially capable of replacing semiconductor QDs, but with the advantage of much lower toxicity.

In semiconductors, light absorption generally leads to an electron being excited from the valence to the conduction band, leaving behind a hole. The electron and the hole can bind to each other to form an exciton. When this exciton recombines (i.e. the electron resumes its ground state), the exciton"s energy can be emitted as light. This is called fluorescence. In a simplified model, the energy of the emitted photon can be understood as the sum of the band gap energy between the highest occupied level and the lowest unoccupied energy level, the confinement energies of the hole and the excited electron, and the bound energy of the exciton (the electron–hole pair):

As the confinement energy depends on the quantum dot"s size, both absorption onset and fluorescence emission can be tuned by changing the size of the quantum dot during its synthesis. The larger the dot, the redder (lower energy) its absorption onset and fluorescence spectrum. Conversely, smaller dots absorb and emit bluer (higher energy) light. Recent articles in

To improve fluorescence quantum yield, quantum dots can be made with shells of a larger bandgap semiconductor material around them. The improvement is suggested to be due to the reduced access of electron and hole to non-radiative surface recombination pathways in some cases, but also due to reduced Auger recombination in others.

Quantum dots are particularly promising for optical applications due to their high extinction coefficientsingle-electron transistor and show the Coulomb blockade effect. Quantum dots have also been suggested as implementations of qubits for quantum information processing,

Tuning the size of quantum dots is attractive for many potential applications. For instance, larger quantum dots have a greater spectrum-shift toward red compared to smaller dots and exhibit less pronounced quantum properties. Conversely, the smaller particles allow one to take advantage of more subtle quantum effects.

Being zero-dimensional, quantum dots have a sharper density of states than higher-dimensional structures. As a result, they have superior transport and optical properties. They have potential uses in diode lasers, amplifiers, and biological sensors.plasmon resonance in the photoluminescent excitation spectrum of (CdSe)ZnS nanocrystals. High-quality quantum dots are well suited for optical encoding and multiplexing applications due to their broad excitation profiles and narrow/symmetric emission spectra. The new generations of quantum dots have far-reaching potential for the study of intracellular processes at the single-molecule level, high-resolution cellular imaging, long-term in vivo observation of cell trafficking, tumor targeting, and diagnostics.

In December 2019, Robert S. Langer and his team developed and patented a technique whereby transdermal patches could be used to label people with invisible ink to store information subcutaneously. This was presented as a boon to "developing nations" where lack of infrastructure means an absence of medical records.Massachusetts Institute of Technology,dye that is delivered, in this case along with a vaccine, by a microneedle patch." The research "was funded by the Bill and Melinda Gates Foundation and the Koch Institute for Integrative Cancer Research."

In modern biological analysis, various kinds of organic dyes are used. However, as technology advances, greater flexibility in these dyes is sought.photobleaching).blinking of quantum dots is a minor drawback. However, there have been groups which have developed quantum dots which are essentially nonblinking and demonstrated their utility in single molecule tracking experiments.

Semiconductor quantum dots have also been employed for in vitro imaging of pre-labeled cells. The ability to image single-cell migration in real time is expected to be important to several research areas such as embryogenesis, cancer metastasis, stem cell therapeutics, and lymphocyte immunology.

One application of quantum dots in biology is as donor fluorophores in Förster resonance energy transfer, where the large extinction coefficient and spectral purity of these fluorophores make them superior to molecular fluorophores

The use of quantum dots for tumor targeting under in vivo conditions employ two targeting schemes: active targeting and passive targeting. In the case of active targeting, quantum dots are functionalized with tumor-specific binding sites to selectively bind to tumor cells. Passive targeting uses the enhanced permeation and retention of tumor cells for the delivery of quantum dot probes. Fast-growing tumor cells typically have more permeable membranes than healthy cells, allowing the leakage of small nanoparticles into the cell body. Moreover, tumor cells lack an effective lymphatic drainage system, which leads to subsequent nanoparticle-accumulation.

Quantum dot probes exhibit in vivo toxicity. For example, CdSe nanocrystals are highly toxic to cultured cells under UV illumination, because the particles dissolve, in a process known as photolysis, to release toxic cadmium ions into the culture medium. In the absence of UV irradiation, however, quantum dots with a stable polymer coating have been found to be essentially nontoxic.Hydrogel encapsulation of quantum dots allows for quantum dots to be introduced into a stable aqueous solution, reducing the possibility of cadmium leakage. Then again, only little is known about the excretion process of quantum dots from living organisms.

In another potential application, quantum dots are being investigated as the inorganic fluorophore for intra-operative detection of tumors using fluorescence spectroscopy.

Delivery of undamaged quantum dots to the cell cytoplasm has been a challenge with existing techniques. Vector-based methods have resulted in aggregation and endosomal sequestration of quantum dots while electroporation can damage the semi-conducting particles and aggregate delivered dots in the cytosol. Via cell squeezing, quantum dots can be efficiently delivered without inducing aggregation, trapping material in endosomes, or significant loss of cell viability. Moreover, it has shown that individual quantum dots delivered by this approach are detectable in the cell cytosol, thus illustrating the potential of this technique for single molecule tracking studies.

The tunable absorption spectrum and high extinction coefficients of quantum dots make them attractive for light harvesting technologies such as photovoltaics. Quantum dots may be able to increase the efficiency and reduce the cost of today"s typical silicon photovoltaic cells. According to an experimental report from 2004,lead selenide can produce more than one exciton from one high energy photon via the process of carrier multiplication or multiple exciton generation (MEG). This compares favorably to today"s photovoltaic cells which can only manage one exciton per high-energy photon, with high kinetic energy carriers losing their energy as heat. Quantum dot photovoltaics would theoretically be cheaper to manufacture, as they can be made using simple chemical reactions.

Aromatic self-assembled monolayers (SAMs) (e.g. 4-nitrobenzoic acid) can be used to improve the band alignment at electrodes for better efficiencies. This technique has provided a record power conversion efficiency (PCE) of 10.7%.

Colloidal quantum dots are also used in inorganic/organic hybrid solar cells. These solar cells are attractive because of the potential for low-cost fabrication and relatively high efficiency.2, and Nb2O5 nanomaterials into organic photovoltaics have been commercialized using full roll-to-roll processing.

Another potential use involves capped single-crystal ZnO nanowires with CdSe quantum dots, immersed in mercaptopropionic acid as hole transport medium in order to obtain a QD-sensitized solar cell. The morphology of the nanowires allowed the electrons to have a direct pathway to the photoanode. This form of solar cell exhibits 50–60% internal quantum efficiencies.

Nanowires with quantum dot coatings on silicon nanowires (SiNW) and carbon quantum dots. The use of SiNWs instead of planar silicon enhances the antiflection properties of Si.

Graphene quantum dots have also been blended with organic electronic materials to improve efficiency and lower cost in photovoltaic devices and organic light emitting diodes (OLEDs) in compared to graphene sheets. These graphene quantum dots were functionalized with organic ligands that experience photoluminescence from UV-Vis absorption.

Several methods are proposed for using quantum dots to improve existing light-emitting diode (LED) design, including quantum dot light-emitting diode (QD-LED or QLED) displays, and quantum dot white-light-emitting diode (QD-WLED) displays. Because quantum dots naturally produce monochromatic light, they can be more efficient than light sources which must be color filtered. QD-LEDs can be fabricated on a silicon substrate, which allows them to be integrated onto standard silicon-based integrated circuits or microelectromechanical systems.

Quantum dots are valued for displays because they emit light in very specific gaussian distributions. This can result in a display with visibly more accurate colors.

A conventional color liquid crystal display (LCD) is usually backlit by fluorescent lamps (CCFLs) or conventional white LEDs that are color filtered to produce red, green, and blue pixels. Quantum dot displays use blue-emitting LEDs rather than white LEDs as the light sources. The converting part of the emitted light is converted into pure green and red light by the corresponding color quantum dots placed in front of the blue LED or using a quantum dot infused diffuser sheet in the backlight optical stack. Blank pixels are also used to allow the blue LED light to still generate blue hues. This type of white light as the backlight of an LCD panel allows for the best color gamut at lower cost than an RGB LED combination using three LEDs.

Another method by which quantum dot displays can be achieved is the electroluminescent (EL) or electro-emissive method. This involves embedding quantum dots in each individual pixel. These are then activated and controlled via an electric current application.

The ability of QDs to precisely convert and tune a spectrum makes them attractive for LCD displays. Previous LCD displays can waste energy converting red-green poor, blue-yellow rich white light into a more balanced lighting. By using QDs, only the necessary colors for ideal images are contained in the screen. The result is a screen that is brighter, clearer, and more energy-efficient. The first commercial application of quantum dots was the Sony XBR X900A series of flat panel televisions released in 2013.

In June 2006, QD Vision announced technical success in making a proof-of-concept quantum dot display and show a bright emission in the visible and near infrared region of the spectrum. A QD-LED integrated at a scanning microscopy tip was used to demonstrate fluorescence near-field scanning optical microscopy (NSOM) imaging.

Quantum dot photodetectors (QDPs) can be fabricated either via solution-processing,organic semiconductors. On the other hand, solution-processed QDPs can be readily integrated with an almost infinite variety of substrates, and also postprocessed atop other integrated circuits. Such colloidal QDPs have potential applications in visible- and infrared-light cameras,spectroscopy, and fluorescent biomedical imaging.

Quantum dots also function as photocatalysts for the light driven chemical conversion of water into hydrogen as a pathway to solar fuel. In photocatalysis, electron hole pairs formed in the dot under band gap excitation drive redox reactions in the surrounding liquid. Generally, the photocatalytic activity of the dots is related to the particle size and its degree of quantum confinement.band gap determines the chemical energy that is stored in the dot in the excited state. An obstacle for the use of quantum dots in photocatalysis is the presence of surfactants on the surface of the dots. These surfactants (or ligands) interfere with the chemical reactivity of the dots by slowing down mass transfer and electron transfer processes. Also, quantum dots made of metal chalcogenides are chemically unstable under oxidizing conditions and undergo photo corrosion reactions.

Quantum dots are theoretically described as a point-like, or zero dimensional (0D) entity. Most of their properties depend on the dimensions, shape, and materials of which QDs are made. Generally, QDs present different thermodynamic properties from their bulk materials. One of these effects is melting-point depression. Optical properties of spherical metallic QDs are well described by the Mie scattering theory.

3D confined electron wave functions in a quantum dot. Here, rectangular and triangular-shaped quantum dots are shown. Energy states in rectangular dots are more s-type and p-type. However, in a triangular dot the wave functions are mixed due to confinement symmetry. (Click for animation)

In a semiconductor crystallite whose size is smaller than twice the size of its exciton Bohr radius, the excitons are squeezed, leading to quantum confinement. The energy levels can then be predicted using the particle in a box model in which the energies of states depend on the length of the box. Comparing the quantum dot"s size to the Bohr radius of the electron and hole wave functions, 3 regimes can be defined. A "strong confinement regime" is defined as the quantum dots radius being smaller than both electron and hole Bohr radius, "weak confinement" is given when the quantum dot is larger than both. For semiconductors in which electron and hole radii are markedly different, an "intermediate confinement regime" exists, where the quantum dot"s radius is larger than the Bohr radius of one charge carrier (typically the hole), but not the other charge carrier.

Splitting of energy levels for small quantum dots due to the quantum confinement effect. The horizontal axis is the radius, or the size, of the quantum dots and ab* is the Exciton Bohr radius.

where aB=0.053 nm is the Bohr radius, m is the mass, μ is the reduced mass, and εr is the size-dependent dielectric constant (Relative permittivity). This results in the increase in the total emission energy (the sum of the energy levels in the smaller band gaps in the strong confinement regime is larger than the energy levels in the band gaps of the original levels in the weak confinement regime) and the emission at various wavelengths. If the size distribution of QDs is not enough peaked, the convolution of multiple emission wavelengths is observed as a continuous spectra.

The exciton entity can be modeled using the particle in the box. The electron and the hole can be seen as hydrogen in the Bohr model with the hydrogen nucleus replaced by the hole of positive charge and negative electron mass. Then the energy levels of the exciton can be represented as the solution to the particle in a box at the ground level (n = 1) with the mass replaced by the reduced mass. Thus by varying the size of the quantum dot, the confinement energy of the exciton can be controlled.

There is Coulomb attraction between the negatively charged electron and the positively charged hole. The negative energy involved in the attraction is proportional to Rydberg"s energy and inversely proportional to square of the size-dependent dielectric constant

{\displaystyle {\begin{aligned}E_{\textrm {confinement}}&={\frac {\hbar ^{2}\pi ^{2}}{2a^{2}}}\left({\frac {1}{m_{\rm {e}}}}+{\frac {1}{m_{h}}}\right)={\frac {\hbar ^{2}\pi ^{2}}{2\mu a^{2}}}\\E_{\textrm {exciton}}&=-{\frac {1}{\epsilon _{\rm {r}}^{2}}}{\frac {\mu }{m_{\rm {e}}}}R_{y}=-R_{y}^{*}\\E&=E_{\textrm {bandgap}}+E_{\textrm {confinement}}+E_{\textrm {exciton}}\\&=E_{\textrm {bandgap}}+{\frac {\hbar ^{2}\pi ^{2}}{2\mu a^{2}}}-R_{y}^{*}\end{aligned}}}

where μ is the reduced mass, a is the radius of the quantum dot, me is the free electron mass, mh is the hole mass, and εr is the size-dependent dielectric constant.

Although the above equations were derived using simplifying assumptions, they imply that the electronic transitions of the quantum dots will depend on their size. These quantum confinement effects are apparent only below the critical size. Larger particles do not exhibit this effect. This effect of quantum confinement on the quantum dots has been repeatedly verified experimentally

A variety of theoretical frameworks exist to model optical, electronic, and structural properties of quantum dots. These may be broadly divided into quantum mechanical, semiclassical, and classical.

Semiclassical models of quantum dots frequently incorporate a chemical potential. For example, the thermodynamic chemical potential of an N-particle system is given by

is the quantum capacitance of a quantum dot, where we denoted by I(N) the ionization potential and by A(N) the electron affinity of the N-particle system.

Classical models of electrostatic properties of electrons in quantum dots are similar in nature to the Thomson problem of optimally distributing electrons on a unit sphere.

The classical electrostatic treatment of electrons confined to spherical quantum dots is similar to their treatment in the Thomson,plum pudding model, of the atom.

The classical treatment of both two-dimensional and three-dimensional quantum dots exhibit electron shell-filling behavior. A "periodic table of classical artificial atoms" has been described for two-dimensional quantum dots.

Murray, C. B.; Kagan, C. R.; Bawendi, M. G. (2000). "Synthesis and Characterization of Monodisperse Nanocrystals and Close-Packed Nanocrystal Assemblies". 30 (1): 545–610. Bibcode:2000AnRMS..30..545M. doi:10.1146/annurev.matsci.30.1.545.

Lodahl, Peter; Mahmoodian, Sahand; Stobbe, Søren (2015). "Interfacing single photons and single quantum dots with photonic nanostructures". Reviews of Modern Physics. 87 (2): 347–400. arXiv:Bibcode:2015RvMP...87..347L. doi:10.1103/RevModPhys.87.347. ISSN 0034-6861. S2CID 118664135.

Senellart, Pascale; Solomon, Glenn; White, Andrew (2017). "High-performance semiconductor quantum-dot single-photon sources". Nature Nanotechnology. 12 (11): 1026–1039. Bibcode:2017NatNa..12.1026S. doi:10.1038/nnano.2017.218. ISSN 1748-3387. PMID 29109549.

Michalet, X.; Pinaud, F. F.; Bentolila, L. A.; Tsay, J. M.; Doose, S.; Li, J. J.; Sundaresan, G.; Wu, A. M.; Gambhir, S. S.; Weiss, S. (2005). "Quantum Dots for Live Cells, in Vivo Imaging, and Diagnostics". Science. 307 (5709): 538–44. Bibcode:2005Sci...307..538M. doi:10.1126/science.1104274. PMC PMID 15681376.

Gorbachev, I. A.; Goryacheva, I. Yu; Glukhovskoy, E. G. (1 June 2016). "Investigation of Multilayers Structures Based on the Langmuir-Blodgett Films of CdSe/ZnS Quantum Dots". BioNanoScience. 6 (2): 153–156. doi:10.1007/s12668-016-0194-0. ISSN 2191-1630. S2CID 139004694.

Achermann, Marc; Petruska, Melissa A.; Crooker, Scott A.; Klimov, Victor I. (1 December 2003). "Picosecond Energy Transfer in Quantum Dot Langmuir−Blodgett Nanoassemblies". The Journal of Physical Chemistry B. 107 (50): 13782–13787. arXiv:Bibcode:2003cond.mat.10127A. doi:10.1021/jp036497r. ISSN 1520-6106. S2CID 97571829.

Mangolini, L.; Thimsen, E.; Kortshagen, U. (2005). "High-yield plasma synthesis of luminescent silicon nanocrystals". Nano Letters. 5 (4): 655–659. Bibcode:2005NanoL...5..655M. doi:10.1021/nl050066y. PMID 15826104.

Knipping, J.; Wiggers, H.; Rellinghaus, B.; Roth, P.; Konjhodzic, D.; Meier, C. (2004). "Synthesis of high purity silicon nanoparticles in a low Pressure microwave reactor". Journal of Nanoscience and Nanotechnology. 4 (8): 1039–1044. doi:10.1166/jnn.2004.149. PMID 15656199. S2CID 2461258.

Kortshagen, U (2009). "Nonthermal plasma synthesis of semiconductor nanocrystals". J. Phys. D: Appl. Phys. 42 (11): 113001. Bibcode:2009JPhD...42k3001K. doi:10.1088/0022-3727/42/11/113001. S2CID 121602427.

Pi, X. D.; Kortshagen, U. (2009). "Nonthermal plasma synthesized freestanding silicon–germanium alloy nanocrystals". Nanotechnology. 20 (29): 295602. Bibcode:2009Nanot..20C5602P. doi:10.1088/0957-4484/20/2